2.4.2.1 Analogien zu elektrischen Bauelementen

Unter bestimmten Voraussetzungen verhält sich ein System aus Körpern, die eine Wärmekapazität haben und sich berühren, sodass Wärmeleitung auftritt, ähnlich wie ein elektrisches System aus Kondensatoren und Widerständen. Eine der Voraussetzungen ist, dass die Wärmeleitfähigkeit innerhalb der wärmespeichernden Körper jeweils sehr gut ist im Vergleich zu den Übergangswiderständen zu den angrenzenden Körpern.

Bei der Berechnung des thermischen Verhaltens der Elektromaschine, ergeben sich  Wärmestromquellen aus den elektrischen Verlustleistungen. Da auch während eines Aufwärmvorgangs Wärme durch das Material hindurchfließt, ist der Wärmestrom, der in eine thermische Masse hineinfließt, die Summe aus der abfließenden Wärme und der für eine Temperaturänderung bei gegebener Wärmekapazität der Masse erforderlichen Wärme. Ein elektrisches Modell, das diesen Vorgang nachbildet, besteht für jede thermische Masse aus einer Stromquelle, einem Kondensator als Speicher und einem parallel geschalteten Ohm´schen Widerstand, über den Strom zum nächsten Bauteil oder direkt zur „Erde“  abfließt.

2.4.2.2 Erstellung eines thermischen Modells mit drei Massen

Übertragen auf die zu berechnende Art von PM-Maschinen wird ein Modell erstellt, das drei thermische Massen aufweist (siehe Bild 7): 1. Rotor, 2. Wickelköpfe, 3. Rest des Stators ohne die Wickelköpfe: Nutbereiche, Blechpaket und Kühlmantel.

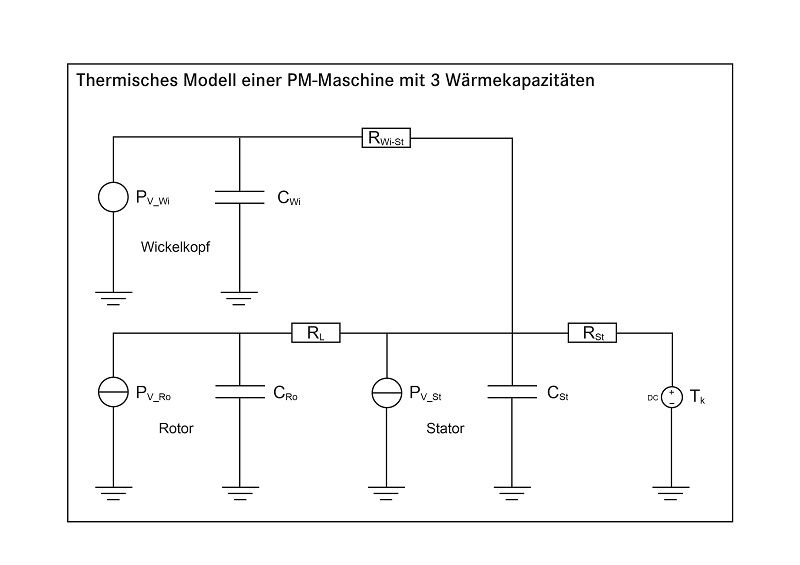
Bild 7: Thermisches Modell einer PM-Maschine mit drei Wärmekapazitäten © Prof. Dr. Ulrich Schrade

Die Zusammenfassung des in den Nuten befindlichen Kupfers, des Isolier- und Tränklackes dazwischen, des Blechpakets sowie des Aluminiumgehäuses mit seinen Kühlkanälen zu einer thermischen Masse, kurz „Stator-Masse“ ist eine Vereinfachung, die noch zulässig erscheint, weil das Temperaturgefälle innerhalb dieser Bauteile, verglichen mit dem Temperaturunterschied zu den Wickelköpfen, relativ flach ist (siehe Bild 6). Die Wärmekapazität des Stators CSt ergibt sich als Summe der Wärmekapazitäten der enthaltenen Materialien, jeweils multipliziert mit den anteiligen Massen. Ihre Temperatur TSt bezieht sich auf den arithmetischen Mittelwert über der aktiven Länge für den wärmsten Kupferleiter in der Nut, wie er im Schichtmodell berechnet wird. Der thermische Widerstand RSt wird aus der Temperaturdifferenz  zum Kühlwasser und dem Wärmestrom  aus der gesamten Verlustleistung von Wickelköpfen und Stator ermittelt:

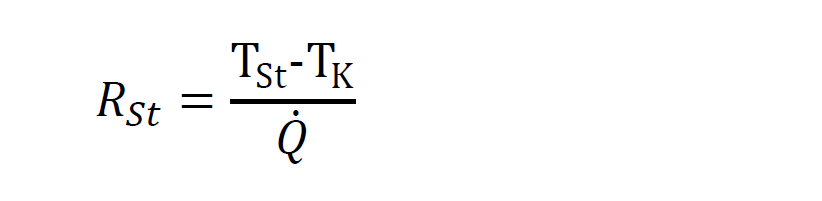
Die Verlustleistung im Stator PV_St enthält Anteile aus Eisen- und Kupferverlusten. Die Wickelköpfe mit der Verlustleistung PV_Wi (nur anteilige Kupferverluste) und der Wärmekapazität CWi sind über den thermischen Widerstand RWi-St angebunden, bei dessen Ermittlung sowohl die Temperaturerhöhung am Nutanfang bzw. Nutende, wo die Wickelköpfe angebunden sind als auch der Temperaturunterschied von dort zum wärmsten Punkt in der Mitte der einzelnen Drahtschleifen der Wickelköpfe berücksichtigt sind.

Um auch die Verluste im Rotor und zu erfassen und seine Temperatur TRo berechnen zu können, enthält das Modell die zugehörige Verlustleistungsquelle PV_Ro und eine Masse mit der Wärmekapazität CRo. Der Luftspalt wird als Wärmeleitungswiderstand RL modelliert. 

2.4.2.3 Differentialgleichungen für drei thermische Massen

Die von einer Masse aufgenommene (bei negativem Vorzeichen abgegebene) Wärmeleistung P ist gleich dem Produkt aus Wärmekapazität C und zeitlicher Temperaturänderung:

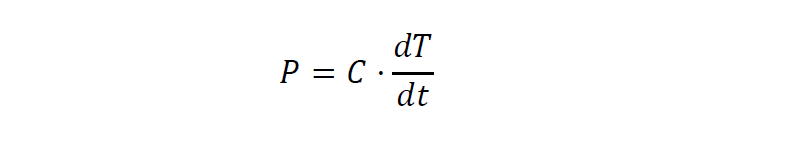
Das Produkt aus Wärmeleitungswiderstand R und durchfließender Wärmeleistung P ist die Temperaturdifferenz

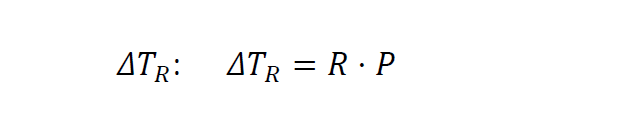
Der gesuchte Temperatur-Vektor enthält die Temperaturen von Wickelkopf, Stator und Rotor. Die Eingangsgrößen der Berechnung im Vektor sind die Verlustleistungen der Wickelköpfe P_{V_Wi}, im Stator P_{V_St}, im Rotor P_{V_Ro} und die Kühlwassertemperatur T_K.

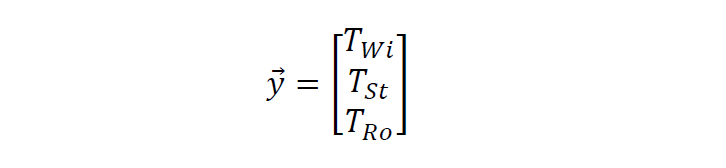
Das Modell erfordert die Berechnung des folgenden Differentialgleichungssystems:

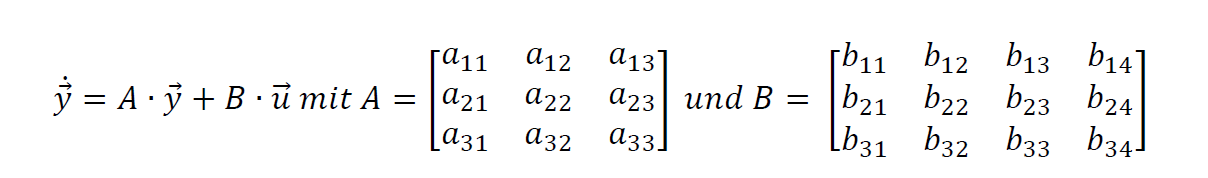
Die Einflusszahlen a_ij und b_ik enthalten Terme aus den für die Maschine spezifischen Wärmekapazitäten und Wärmewiderständen, die aus dem statischen Rechenmodell abgeleitet werden; etliche sind null. Das Verfahren kann auch auf eine größere Zahl von thermischen Massen erweitert werden. Ein Modell mit vier Massen wird derzeit entwickelt.

2.5 Rechenergebnisse

Bild 8 zeigt eine Simulation des Erwärmungsvorganges der Beispiel-Maschine mit folgenden Anfangstemperaturen: Rotor: 27,0 °C, Stator und Wickelkopf: 30,0 °C. Die Kühlwassertemperatur wird auf 30,0 °C konstant gehalten. Die Verlustleistung ist 100 Sekunden lang null und springt dann auf folgende Werte: Kupferverluste 2.038 W, Eisenverluste 182 W, in Summe also 2.220 W. Dieses einfache Beispiel zeigt, wie die Temperatur des Wickelkopfs schneller ansteigt und höhere Werte erreicht als die des Stators. Beide Temperaturen nähern sich den in der stationären Rechnung ermittelten Beharrungstemperaturen (siehe Bild 6).

Die Rotor-Temperatur steigt nur sehr langsam an, da am Rotor eine Verlustleistung von nur 22,4 W angesetzt wurde (1 % der Gesamtverluste) und weil der Luftspalt einen sehr großen thermischen Widerstand hat, sodass kaum Wärme vom Stator zum Rotor abgeleitet wird.

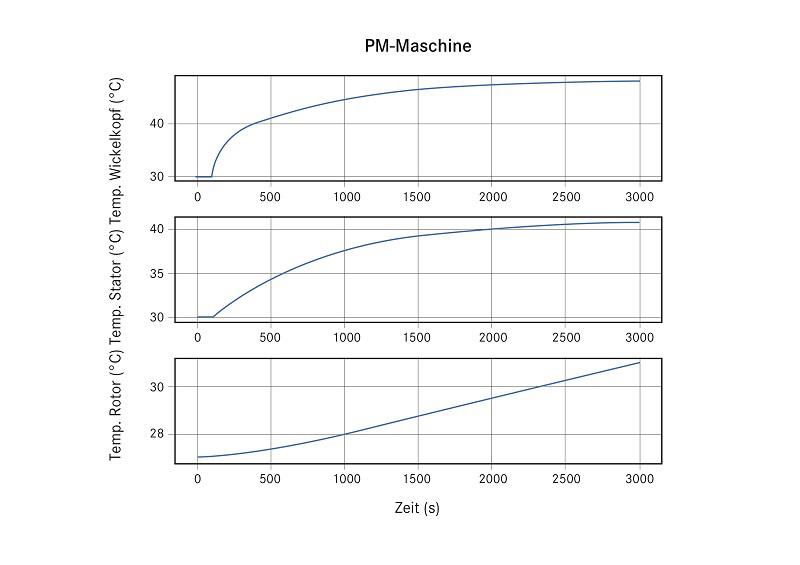
Bild 8: Simulation des Erwärmungsvorgangs einer PM-Maschine © Prof. Dr. Ulrich Schrade

3. Zusammenfassung und Ausblick

Das Simulationstool ist so weit entwickelt, dass Temperaturberechnungen im Zeitbereich durchgeführt werden können. Die zeitlich veränderliche Verlustleistung, aufgeteilt in Eisen- und Kupferverluste, wird aus der Streckenfahrt-Simulation heraus ermittelt.

In nächster Zeit werden mehrere Motoren auf einem Lastprüfstand mit – aus der Streckenfahrt Simulation abgeleiteten - Lastkollektiven gefahren, sodass realitätsnahe Einsatzbedingungen vorliegen. Die Messung der relevanten Wicklungstemperaturen bei diesen Versuchen wird Daten für die Kalibrierung des Simulationstools liefern. Dabei soll auch untersucht werden, ob ein Modell mit vier thermischen Massen genauere Ergebnisse liefern kann als das bestehende Modell mit drei Massen.