Während der Fahrt mit leerem Akku „liegen“ bleiben - das will kein E-Bike-Fahrer. Idealerweise soll die geplante Strecke ohne Unterschreitung der verfügbaren Akkukapazität schnellstmöglich zurückzulegt werden können. Die Lösung hierfür könnte eine optimerte Unterstützungssteuerung für E-Bikes sein, die auf dem sogenannten CMSC-Verfahren beruht. Wie das funktioniert, erklären unsere Gastautoren.
1. Einleitung
Elektrofahrräder können derzeit ein starkes Marktwachstum sowie eine Zunahme der Popularität aufweisen. Zusätzlich kommt es durch den Klimawandel zu einer verstärkten Elektrifizierung der Mobilität. Davon profitiert das Elektrofahrrad besonders in staugeplagten urbanen Regionen und als attraktive Art der Freizeitgestaltung [1]–[7]. Eines der Hauptprobleme von Elektrofahrrädern und der Elektromobilität im Allgemeinen ist die beschränkte Akkukapazität und die daraus resultierende limitierte Reichweite in Kombination mit einer langen Ladedauer [5]. Dies führt zur sogenannten „Reichweitenangst“ des Fahrers des Elektrofahrzeugs. Dabei handelt es sich um die Befürchtung, während der Fahrt aufgrund eines leeren Akkus „liegen“ zu bleiben [8]. Lösungen zur Bekämpfung der Reichweitenangst bei Elektrofahrrädern stellen oftmals lediglich eine Verschiebung des Problems zu größeren Reichweiten dar. So kann beispielsweise durch Rekuperation eine gewisse Reichweitensteigerung erzielt werden [9], [10]. Alternativ können Akkus mit größerer Kapazität eingesetzt werden. Beides bringt wiederum Nachteile (Kosten, Gewicht, …) mit sich und stellt keine nachhaltige Lösung des Problems der Reichweitenangst dar.
Zur Reduzierung der Reichweitenproblematik bei Elektrofahrrädern soll die optimale Unterstützungsstrategie ermittelt werden, die dem Fahrer ermöglicht, unter Einhaltung der beschränkten Akkukapazität eine geplante Strecke in minimaler Zeit zu absolvieren. Dafür wird ein Modell eines Elektrofahrrads erstellt (siehe Abschnitt 2), welches mithilfe eines Optimierungsalgorithmus untersucht wird (siehe Abschnitt 3). Die ermittelte Lösung wird sowohl im Modell als auch im Fahrversuch einem Vergleich zu herkömmlichen Fahrmodi unterzogen, um das erzielte Ergebnis der optimierten Strategie experimentell zu validieren (siehe Abschnitt 4). In einer Diskussion wird auf das Potenzial und die Umsetzbarkeit auf dem Elektrofahrrad zur automatisierten Unterstützungssteuerung eingegangen (siehe Abschnitt 5). Abschließend werden die Ergebnisse zusammengefasst und ein Ausblick zeigt zukünftige Forschungsfelder auf (siehe Abschnitt 6). Sämtliche Untersuchungen erfolgen anhand des Bosch eBike Systems.
2. Modellbildung
Betrachtet werden sogenannte Pedelecs (Pedal Electric Cycles), welche mit einer Kombination aus menschlicher und elektrischer Leistung angetrieben werden [3]. Aus diesem Grund wird auch von einem human-electric hybrid [11] gesprochen, einem mechanisch gekoppelten, parallelen Hybrid aus Mensch und elektrischer Maschine [12]. Ein ausschließlich elektrischer Betrieb ist gesetzlich bedingt nicht möglich [13]. Die Motorleistung PMotor ergibt sich ergibt sich nach (1) aus der Fahrerleistung PFahrer sowie dem Unterstützungsfaktor xassist. Eine alleinige Leistungseinbringung durch den Fahrer, wie bei einem herkömmlichen Fahrrad, ist weiterhin möglich (xassist = 0). Die eingebrachte Antriebsleistung PSystem ist die Kombination aus Fahrerund Motorleistung (2).
PMotor = PFahrer ∙ xassist (1)
PSystem = PFahrer + PMotor = PFahrer ∙ (1 + xassist) (2)
2.1 Beschreibung der Längsdynamik
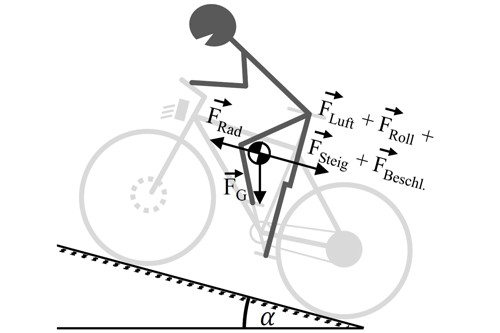
Während der Fahrt des Elektrofahrrads muss je nach Fahrsituation eine Antriebsleistung am Hinterrad PRad aufgebracht werden. Diese entspricht der eingebrachten Systemleistung abzüglich der Wirkungsgradverluste im Antriebsstrang hAntrieb (3). Die benötigte Antriebsleistung ergibt sich aus der Widerstandskraft FWid. als Summe aus Luft-FLuft, Roll-FRoll, Steigungs-FSteig und Beschleunigungswiderstand FBeschl. (4). Diese wirkt der antreibenden Kraft FRad, die sich aus der eingebrachten Antriebsleistung am Hinterrad ergibt (5), entgegen. Bild 1 stellt diesen Zusammenhang für eine allgemeine Fahrsituation exemplarisch dar [14].
PRad = PSystem ∙ hAntrieb (3)
FWid = FLuft + FRoll + FSteig + FBeschl. (4)
FRad = PRad ∙ veBike (5)
![Bild 1: Fahrwiderstände am Elektrofahrrad (FG: Gewichtskraft, a: Fahrbahnsteigung) [9]. Bild 1: Fahrwiderstände am Elektrofahrrad (FG: Gewichtskraft, a: Fahrbahnsteigung) [9].](/images/eMobilJournal/2019/03_2019/Unterstützung_Ebike/B1-Fahrwiderstände-eBike-b.jpg)
Bild 1: Fahrwiderstände am Elektrofahrrad (FG: Gewichtskraft, a: Fahrbahnsteigung) [9].
2.2 Beschreibung des Energieverbrauchs
Die Leistung der Batterie PBat ergibt sich aus der benötigten Motorleistung PMotor unter Berücksichtigung der Wirkungsgrade des Motors hMotor sowie des Kabels hKabel zwischen Motor und Batterie (6). Daraus kann die der Batterie entnommene Energiemenge EBat berechnet werden (7).
PMotor = PBat ∙ hKabel ∙ hMotor (6)
EBat (t) = ∫ t 0 PBat (s) ds (7)
Die Bestimmung des Ladezustands der Batterie (SoC, engl. State of Charge) ist in der Praxis schwierig, da viele Einflussfaktoren, unteranderem die Temperatur und die durchlaufene Zyklenanzahl, eine Rolle spielen [15]. Aufgrund der Komplexität wird in der Praxis häufig von SoC-Schätzung gesprochen. Hierfür haben sich verschiedene Methoden etabliert [16], [17]. Für die SoC-Bestimmung am Elektrofahrrad kommt hier die Ladungsbilanzierung zum Einsatz. Es werden sämtliche einund ausgehenden Ströme der Batterie IBat integriert und dadurch die Veränderung der Ladungsmenge in der Batterie bilanziert. Mit bekannter verfügbarer Gesamtkapazität Qtot und initialem Ladezustand SoC0 kann der momentan vorliegende SoC ermittelt werden (8) [18].
SoC (t) = SoCo + 1/Qtot • ∫ t 0 PBat (s) ds
2.3 DGL-System zur Optimierung
Mit den vorgestellten Gleichungen kann ein Differentialgleichungssystem (DGL-System) aufgestellt werden, welches das Elektrofahrrad hinsichtlich der Längsdynamik und des Energieverbrauchs für die Optimierung hinreichend genau beschreibt (9). Der Zustandsvektor ist x = [x1, x2, x3]T = [s, veBike, Q]T bzw. x˙ = [x˙1, x˙2, x˙3]T = [veBike, aeBike, IBat]T mit der zurückgelegten Strecke s, der Geschwindigkeit veBike, der Beschleunigung aeBike sowie der Ladungsmenge Q und dem Batteriestrom IBat.
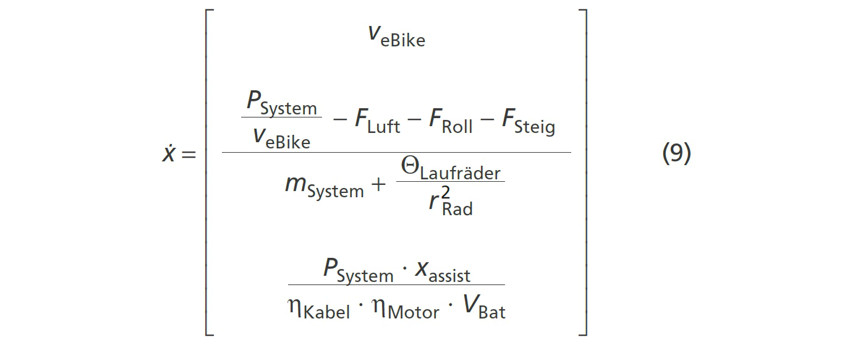
Die zweite Gleichung beschreibt die Längsdynamik und ist mithilfe des Beschleunigungswiderstands nach der Beschleunigung des Elektrofahrrads aeBike aufgelöst (10). Hierbei werden die translatorische Trägheit aufgrund der Masse des Systems mSystem, sowie die größten rotatorischen Trägheitsmomente der Laufräder QLaufräder, welche mithilfe des Radius rRad in eine translatorische Kraft konvertiert werden, mitberücksichtigt. Die dritte Gleichung des DGL-Systems beschreibt den Energieverbrauch. Dabei wird zusätzlich die Batteriespannung VBat benötigt. Diese ist im Rahmen der Optimierung als konstant angesetzt. Mithilfe des DGL-Systems wird die Optimierung durchgeführt. Die Kalibrierung und Validierung des Modells ist in [19] näher beschrieben.
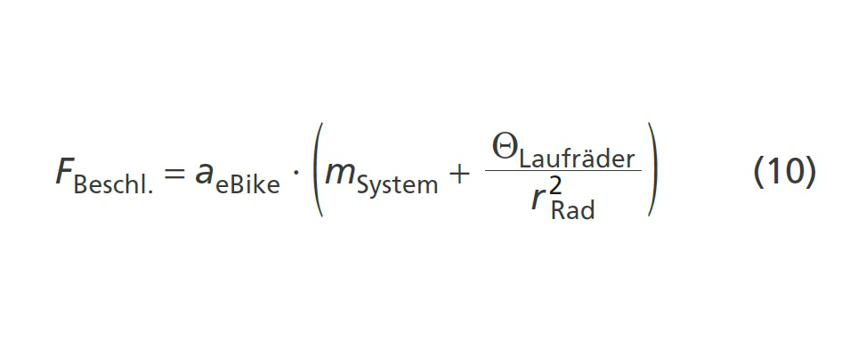
3. Optimierung
In diesem Abschnitt wird das Optimierungsproblem vorgestellt, bevor der verwendete Optimierungsalgorithmus sowie die erzielten Ergebnisse näher betrachtet werden.
3.1 Optimierungsproblem
Das Ziel der Optimierung ist es, Erkenntnisse hinsichtlich der optimalen Unterstützungssteuerung von Elektrofahrrädern im Modell zu erhalten und damit die Basis für eine mögliche Implementierung auf dem Elektrofahrrad zu generieren. Hierbei soll eine vorgegebene Strecke mit beschränkter Energiemenge des Akkus in möglichst kurzer Zeit zurückgelegt werden. Daraus ergibt sich mit dem in (9) beschriebenen DGL-System folgendes nichtlineares Optimierungsproblem
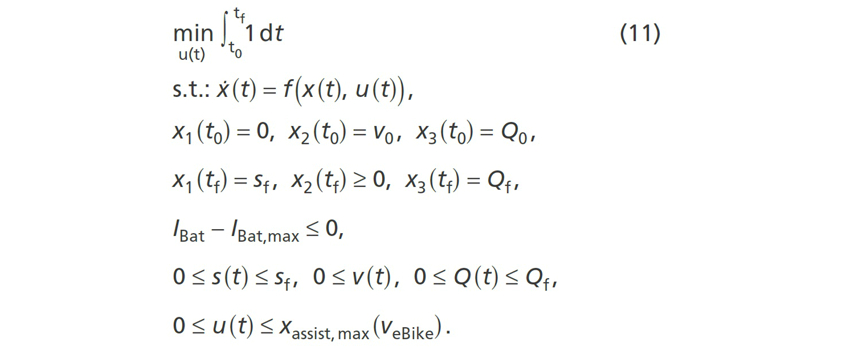
Die Steuervariable u ist der Unterstützungsfaktor xassist. Die Fahrerleistung PFahrer und die Steigung der Fahrbahn 𝛼 dienen als Modelleingang. Die Zustände zu Beginn der Fahrt (t0) sind durch eine initiale Geschwindigkeit v0 und einen initialen Ladezustand Q0 definiert, die Position ist 0. Am Ende der Fahrt (tf) muss die Endposition der Strecke sf sowie der gewünschte Endladezustand Qf erreicht sein, die Endgeschwindigkeit ist frei. Durch die Ungleichungsnebenbedingung ist der Strom der Batterie hinsichtlich eines Maximalwerts IBat,max beschränkt. Die Steuerung darf einen geschwindigkeitsabhängigen Maximalwert xassist,max, der vom System des Elektrofahrrads sowie dem Gesetzgeber vorgegeben ist (maximale Unterstützungsgeschwindigkeit vassist,max = 25 km/h), nicht überschreiten.
3.2 Optimierungsalgorithmus
Zur Lösung des Optimierungsproblems kommt eine Kombination aus zwei Verfahren, dem Mehrfachschießverfahren und der Kollokation (CMSC-Ansatz, engl. combined multiple shooting with collocation), zum Einsatz. Der CMSC-Ansatz löst das Optimalsteuerungsproblem mithilfe des Mehrfachschießverfahrens und berechnet die Differentialgleichungen, Gradienten und Sensitivitäten mithilfe der Kollokationsmethode [20], [21]. Die Kombination nutzt die Vorteile beider Verfahren und löst das Optimierungsproblem effizient und genau. Es kommt eine Softwarearchitektur des Instituts für Prozessoptimierung der Fakultät Informatik und Automatisierung der TU Ilmenau zum Einsatz [22], [23]. Die Lösung wird mithilfe des Ipopt-Solvers berechnet [24].
Um die Effizienz des verwendeten Verfahrens zu zeigen, wird ein Vergleich zwischen dem CMSC-Ansatz sowie der dynamischen Programmierung (DP) durchgeführt. Die DP wird zur Lösung von Optimalsteuerungsproblemen im Automobilund Fahrradbereich eingesetzt, beispielsweise in [25]–[28]. Der DP-Ansatz wird mit einem Algorithmus des Institute for Dynamic Systems and Control der ETH Zürich realisiert [29]. Das Optimierungsproblem wird mit beiden Verfahren auf derselben Strecke mit den gleichen Randbedingungen gelöst. Die Diskretisierung erfolgt über die Strecke in 5m-Schritten und nicht wie üblich über die Zeit. Der Grund hierfür liegt darin, dass die Modelleingänge PFahrer und a in Abhängigkeit der Strecke s vorliegen und die Zeit das Optimierungsziel darstellt. Die Lösungen sind identisch, jedoch kann mithilfe des CMSC-Verfahrens das Problem fast achtmal schneller gelöst werden als mithilfe des verwendeten DP-Ansatzes (siehe Tabelle 1). Dies bestätigt die Effizienz des CMSC-Verfahrens, welches im Weiteren verwendet wird.

Nun werden die Rechenzeit und das Konvergenzverhalten des CMSC-Verfahrens näher betrachtet, indem Strecken unterschiedlicher Länge berechnet und die Eingangsparameter PFahrer und a wahlweise konstant gehalten bzw. variiert werden. Eine Zusammenfassung der Ergebnisse gibt Tabelle 2. Hierbei handelt es sich lediglich um Trends, die mithilfe der hier durchgeführten empirischen Untersuchungen ermittelt wurden. Mit zunehmender Komplexität und Größe des Optimierungsproblems nimmt die Rechenzeit zu und das Konvergenzverhalten verschlechtert sich. Dieses Verhalten war zu erwarten. Jedoch ist der gewählte Optimierungsalgorithmus geeignet für die geplanten Analysen. Zur Ableitung der optimalen Fahrstrategie genügen Betrachtungen kurzer Strecken mit geringer zur Verfügung stehender Energiemenge, da die Ergebnisse auf längere Strecken übertragen werden können. Zusätzlich sollten die Eingangsparameter getrennt voneinander variiert werden, um den Einfluss dieser besser analysieren zu können. Unter Berücksichtigung dieser Aspekte zeigt sich, dass das CMSC-Verfahren ein effizientes und genaues Verfahren zur Lösung des hier gestellten Optimierungsproblems darstellt.

3.3 Ergebnisse und Folgerungen der Optimierung
Im Folgenden wird exemplarisch das Ergebnis einer durchgeführten Optimierung betrachtet. Das Ziel ist es, Erkenntnisse hinsichtlich der optimalen Unterstützung von Elektrofahrrädern zu gewinnen. Dazu wird eine reale Strecke analysiert, die mit konstanter Fahrerleistung absolviert wird. Der Startwert SoC0 und gewünschte Endwert SoCf des SoCs sind vorgegeben. Die Ergebnisse der Optimierung sind in Bild 2 dargestellt. Es handelt sich um eine Strecke mit ca. 8 km Länge. Neben der Geschwindigkeit sind der SoC, der Unterstützungsfaktor und die stückweise geglättete Steigung abgebildet.
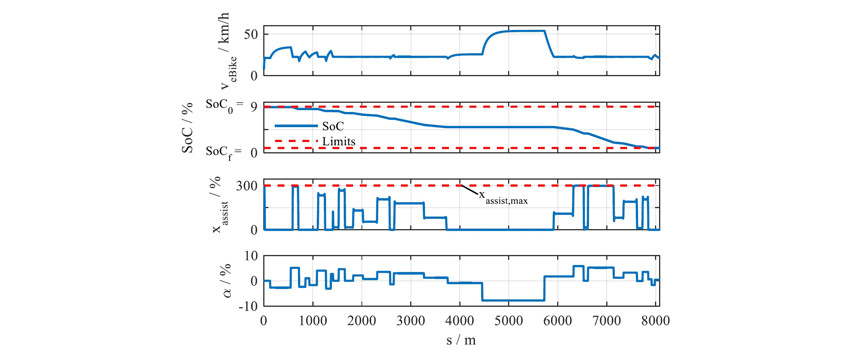
Bild 2: Optimale Steuerung einer realen, geglätteten Strecke.
Es ist zu sehen, dass die zur Verfügung stehende Energiemenge des Akkus vollständig ausgenutzt wird. Dies wurde bei der Problemformulierung der Optimierung so implementiert, ist jedoch hinsichtlich des Ziels der Minimierung der Fahrzeit zu erwarten. Eine schlechtere Energieausnutzung würde zu einer geringeren durchschnittlichen Geschwindigkeit und somit zu einer längeren Fahrzeit führen. Des Weiteren kann festgestellt werden, dass in Bereichen, in denen der Motor den Fahrer unterstützt (xassist > 0), die Geschwindigkeit nahezu konstant ist. Diese optimale Unterstützungsgeschwindigkeit vopt sollte somit bei der Fahrt mit dem Elektrofahrrad angestrebt werden. Das Verhalten ist auf den quadratischen Einfluss der Geschwindigkeit auf den Luftwiderstand zurückzuführen. Eine Erhöhung der Fahrgeschwindigkeit auf einen Wert oberhalb der optimalen Geschwindigkeit würde zu einer überproportionalen Zunahme des Energieverbrauchs führen.
Diese könnte nur mit einer wesentlich stärkeren Reduzierung der Fahrgeschwindigkeit kompensiert werden, was hinsichtlich der Minimierung der Fahrzeit nicht optimal wäre. In Anbetracht dessen ist es optimal, bei einer geringeren verfügbaren Energiemenge die konstante optimale Geschwindigkeit zu verringern, anstatt den Energieverbrauch durch eine starke Reduzierung der Fahrgeschwindigkeit in einem kurzen Bereich zu senken. Aus der Forderung nach konstanter Geschwindigkeit ergibt sich eine Korrelation der Steigung und des Unterstützungsfaktors. Mit Zunahme der Steigung erhöht sich der Fahrwiderstand. Um die konstante Geschwindigkeit zu halten, muss die Antriebsleistung erhöht werden. Bei konstanter Fahrerleistung kann dies lediglich durch Erhöhung der Motorleistung bzw. des Unterstützungsfaktors erfolgen.
Im Weiteren wird der Einfluss variierender Modellparameter untersucht. Da im Betrieb des Elektrofahrrads nicht alle Parameter vorab bekannt sind oder diese sich während der Fahrt ändern können, muss deren Auswirkung auf die optimale Fahrstrategie analysiert werden. Dazu werden die wesentlichen Parameter innerhalb eines realistischen Wertebereichs variiert, vgl. [19]. In Tabelle 3 ist angegeben, um welchen Wert der jeweilige Parameter im Rahmen der Untersuchung erhöht bzw. reduziert wird.
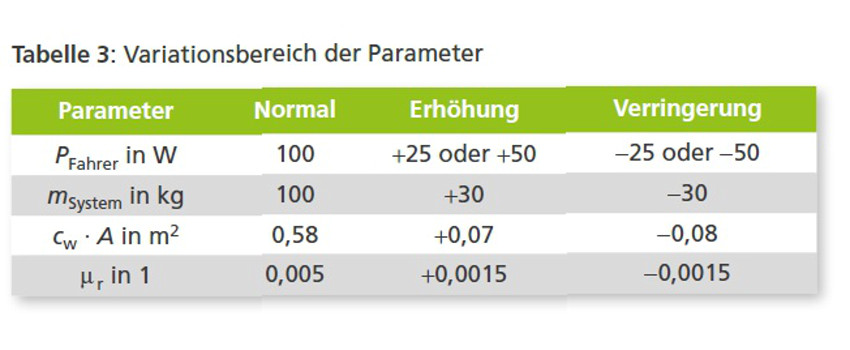
Erzeugt ein abweichender Parameter eine Erhöhung des Fahrwiderstands bzw. verringert sich die Antriebsleistung, muss die Strecke mit einer geringeren optimalen Geschwindigkeit absolviert werden, um den geplanten Energieverbrauch einzuhalten. Bei umgekehrter Beeinflussung erhöht sich die optimale konstante Geschwindigkeit. So wird immer die zur Verfügung stehende Energie bestmöglich ausgenutzt. In Bild 3 sind die SoC-Verläufe verschiedener Parameterkonfigurationen dargestellt. Auffällig ist hierbei, dass die jeweiligen optimalen Entladekurven nur geringe Unterschiede aufweisen. Das heißt, die SoC-Verläufe sind robust gegenüber Parameterschwankungen.
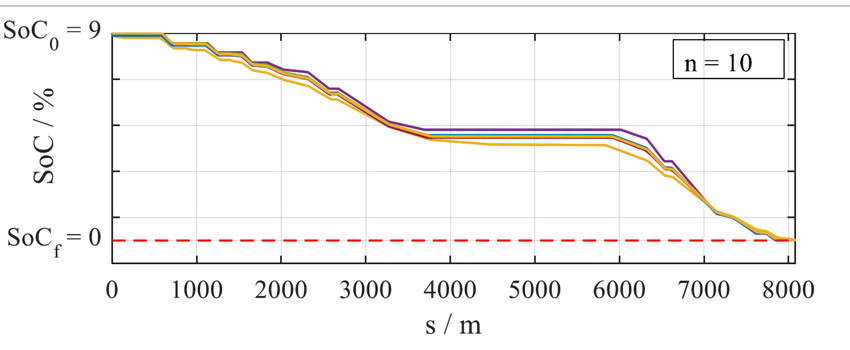
Bild 3: SoC-Trajektorien verschiedener Parameterkonfigurationen
Dies ist dadurch zu erklären, dass beispielsweise ein erhöhter Fahrwiderstand den Energieverbrauch bei gleicher Fahrgeschwindigkeit ebenfalls erhöhen würde. Da die zur Verfügung stehende Energie jedoch beschränkt ist, kann diese Geschwindigkeit nicht gefahren werden. Die optimale Geschwindigkeit muss reduziert werden, wodurch sich der Leistungsbedarf und der Energieverbrauch auch verringern. Das hat zur Folge, dass bei variierenden Parametern die optimalen SoC-Verläufe sich nur geringfügig unterscheiden. Jedoch weisen die optimalen Geschwindigkeiten eine große Varianz auf. Diese Erkenntnis ist hinsichtlich der optimalen Strategie auf dem Elektrofahrrad grundlegend. Somit kann trotz fehlendem Parameterwissen eine Entladekurve aufgestellt werden, die sich dem tatsächlichen optimalen SoC-Verlauf gut annähert.
4. Experimentelle Untersuchung der optimalen Unterstützungsstrategie
Nachdem die optimale Unterstützungssteuerung von Elektrofahrrädern unter idealen Bedingungen ermittelt wurde, werden Vergleiche zu herkömmlichen Fahrmodi aufgestellt. Dafür wird zuerst die optimale Lösung in einem physikalischen Modell in MATLAB/Simscape analysiert. Dieses Modell unterscheidet sich vom oben betrachteten DGL-Modell durch einen höheren Detaillierungsgrad, realistischen Eingangssignalen sowie der Möglichkeit, Störungen aufzubringen. Danach erfolgt eine Betrachtung im realen Fahrversuch.
4.1 Untersuchung der optimalen Lösung im Modell
Durch Simulationen wird die vorab ermittelte optimale Unterstützungssteuerung analysiert und validiert. Hierbei wird die Zeitersparnis der optimierten Strategie im Vergleich zu einem herkömmlichen Fahrmodus bei gleichem Energieverbrauch betrachtet. In einer Simulation wird der Energieverbrauch im „Tour“-Modus (xassist = 120 %) ermittelt. Dieser wird für die Berechnung der optimalen Lösung verwendet. Die so ermittelte Unterstützungsstrategie wird als Modelleingang für eine weitere Simulation eingesetzt. Exemplarisch werden drei Fahrten auf derselben Strecke mit unterschiedlicher Fahrerleistung betrachtet (siehe Tabelle 4).
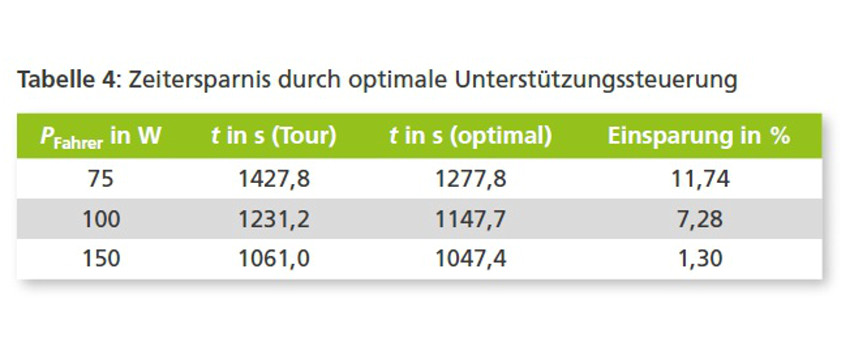
Es ist zu sehen, dass unabhängig von der eingebrachten Leistung des Fahrers die optimierte Fahrstrategie eine kürzere Fahrzeit bei gleichem Energieverbrauch der Batterie ermöglicht. Somit kann gesagt werden, dass die mit dem CMSC-Verfahren ermittelte optimale Lösung eine bessere Fahrstrategie im Vergleich zum herkömmlichen Fahrmodus darstellt. Je nach Fahrerleistung beträgt das Einsparpotenzial über 10 %. Der Vorteil nimmt mit zunehmender Fahrerleistung ab, da die optimale Geschwindigkeit vopt immer weiter ansteigt. Dadurch nähern sich die optimale Strategie und der herkömmliche Fahrmodus einander an. Erreicht vopt den gesetzlich maximal zulässigen Wert, kann sie nicht weiter ansteigen. In diesem Punkt entspricht die optimale Fahrstrategie der des herkömmlichen Fahrmodus. Aus diesem Grund ist das Potenzial bei niedriger Fahrerleistung größer, da die optimierte Fahrstrategie die Unterstützung des Elektrofahrrads stärker beeinflussen und die zur Verfügung stehende Energie zielgerichteter einsetzen kann.
4.2 Untersuchung der optimalen Lösung im realen Fahrversuch
Neben der Simulation soll nun die optimale Lösung des CMSC-Verfahrens im Fahrversuch unter realen Bedingungen betrachtet werden. Hierzu wird eine Referenzfahrt mit einem herkömmlichen Unterstützungsmodus („Eco“-Modus, xassist = 50 %) aufgezeichnet. Anhand der aufgezeichneten Daten wird die Optimierung durchgeführt. Die berechnete Strategie wird wegabhängig auf dem Elektrofahrrad hinterlegt und die Strecke damit nochmals gefahren. Dabei ist darauf zu achten, dass das Fahrverhalten möglichst identisch zu dem der Referenzfahrt gewählt wird. Da die Fahrt unter realen Bedingungen mit Unsicherheiten wie Wind und Verkehr stattfindet, ist eine komplette Übereinstimmung der beiden Fahrten nicht gewährleistet. Aus diesem Grund werden bei der Auswertung (siehe Tabelle 5) sowohl die eingebrachte Fahrerleistung (ØPFahrer), der Energieverbrauch (EVerbrauch) als auch die gefahrene Zeit (t) betrachtet.

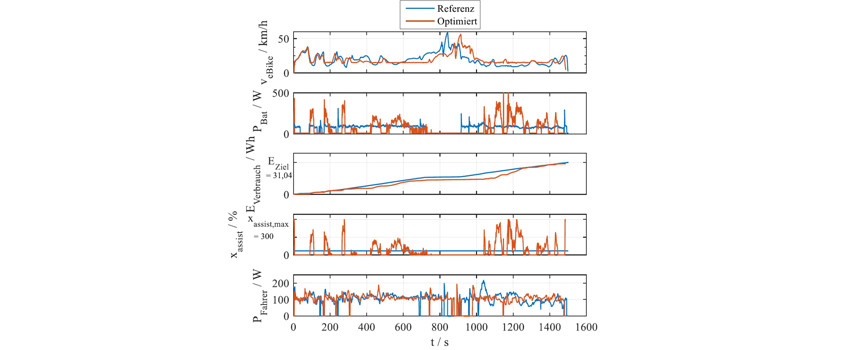
Auch im realen Fahrversuch ist die optimierte Fahrstrategie vorteilhaft gegenüber dem herkömmlichen Unterstützungsmodus. Bei fast identischer durchschnittlicher Eingangsleistung wird die Strecke ca. 1 % schneller und mit 4 % geringerem Energieverbrauch absolviert. Bei gleichem Energieverbrauch wäre somit eine größere Zeitersparnis möglich gewesen. Die Vorteile der optimierten Steuerung werden auch bei Betrachtung der aufgezeichneten Messsignale ersichtlich (siehe Bild 4).
Der ähnliche Verlauf der Fahrerleistung belegt, dass das Fahrverhalten bei den beiden durchgeführten Testfahrten nahezu identisch ist. Bei der optimierten Fahrt ist ein konstanterer Geschwindigkeitsverlauf in den Bereichen mit Motorunterstützung (xassist > 0) erkennbar. Dies ist auf den variablen und optimierten Verlauf des Unterstützungsfaktors zurückzuführen. Dadurch gibt die Batterie die Leistung an die Fahrsituation angepasst ab. Dies führt ebenfalls zu einem variableren Energieverbrauch der Batterie. Im Gegensatz dazu, weist der herkömmliche Fahrmodus mit konstanter Unterstützung eine konstantere Leistungseinbringung und somit auch einen konstanteren Energieverbrauch auf.
Dadurch kann beispielsweise an Anstiegen nur eine geringe Geschwindigkeit erzielt werden, wohingegen in der Ebene mit einer höheren Geschwindigkeit gefahren wird. Wie eingangs analysiert, ist eine konstante Fahrgeschwindigkeit aus energetischer Sicht vorteilhaft. Dies wird von der optimierten Fahrstrategie angestrebt. Dadurch stellt diese eine Verbesserung des Fahrverhaltens dar. Die zur Verfügung stehende Energie wird zielgerichteter eingesetzt als bei den herkömmlichen Fahrmodi, was zu einer gleichmäßigeren Fahrgeschwindigkeit und somit auch zu einem gleichmäßigeren Fahrgefühl führt.
5. Diskussion der Ergebnisse
Wie bei den Untersuchungen im Modell und Fahrversuch ersichtlich wurde, kann durch den optimierten Fahrmodus dieselbe Strecke bei gleichem Energieverbrauch in kürzerer Zeit absolviert werden. Dies ermöglicht dem Fahrer bei beschränkter Akkukapazität die bestmögliche Ausnutzung der zur Verfügung stehenden Energie bei gleichzeitig optimaler Fahrzeit. Das Einsparpotenzial, im Vergleich zu einem herkömmlichen Fahrmodus, lag in einem Bereich von 1 –12 %. Dieser große Bereich zeigt auf, dass eine pauschale Aussage schwierig ist, da viele Faktoren dieses Potenzial beeinflussen. Neben der Strecke haben das Fahrverhalten, die Umweltbedingungen und Fahrradparameter einen Einfluss. Dies entspricht der Aussage der Arbeit von Sciaretta und Guzella zur Regelung von Hybridfahrzeugen in [30], in der eine starke Abhängigkeit des Potenzials vom Fahrzyklus und Fahrzeug erkannt wurde. Allerdings kann als Trend festgestellt werden (siehe Tabelle 6), dass je größer die Einflussmöglichkeiten der optimierten Fahrstrategie sind, das heißt, je stärker diese sich von den herkömmlichen Fahrmodi unterscheiden kann, desto größer ist auch das erzielbare Einsparpotenzial.
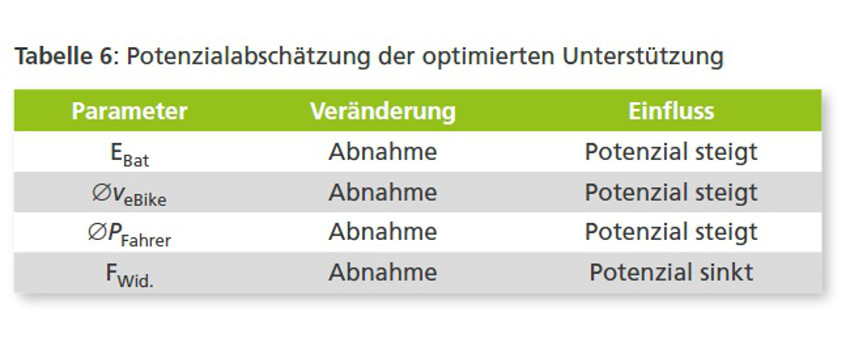
Umsetzbarkeit auf dem Elektrofahrrad
Bei Betrachtung der erzielten Ergebnisse der optimierten Fahrstrategie kann diese bei entsprechender Umsetzung auf dem Elektrofahrrad zur Bekämpfung der Reichweitenangst des Fahrers des Elektrofahrrads beitragen. Hinsichtlich der Reichweitenangst stehen für den Nutzer das Einhalten der zur Verfügung stehenden Energie und damit das sichere Ankommen am gewünschten Ziel im Fokus, die Zeitoptimalität ist zweitrangig. Hierbei ist die gewonnene Erkenntnis hinsichtlich der robusten SoC-Trajektorie von entscheidender Bedeutung. Basierend auf der SoC-Trajektorie kann ein Regler entworfen werden, der die Unterstützung des Elektrofahrrads entsprechend dem tatsächlichen Energieverbrauch, selbst bei unbekannten Parametern, einstellt. Allerdings stellt die Berechnung der SoC-Trajektorie für den Einsatz auf dem Elektrofahrrad ein Problem dar. Selbst der effiziente CMSC-Ansatz benötigt bereits bei kurzen Strecken auf einem leistungsstarken Computer mehrere Minuten. Dies ist ein Ausschlusskriterium für den Einsatz auf dem Elektrofahrrad.
Abhilfe könnte eine vereinfachte Berechnung schaffen, die unter Annahmen die optimale Lösung annähert und eine schnellere Berechnung ermöglicht. Alternativ kann die Planung nur für kurze Strecken implementiert werden, um am Ende der Strecke die Optimalität sowie die Einhaltung des Energieverbrauchs sicherzustellen. Eine serverbasierte Berechnung der optimalen Strategie in leistungsstarken Rechenzentren und anschließende drahtlose Übertragung auf das Elektrofahrrad könnten ebenfalls eine mögliche Lösung für das Problem darstellen. Jedoch müssten dafür die Elektrofahrräder mit entsprechenden Empfangsmodulen ausgestattet werden. Dieses Problem muss zukünftig angegangen werden, um eine automatisierte und optimierte Unterstützungssteuerung zu ermöglichen und dadurch eine Minderung der Reichweitenangst des Nutzers sowie eine größere Verbreitung von Elektrofahrrädern zu erreichen.
6. Zusammenfassung und Ausblick
Mit dieser Arbeit wurde ein Beitrag zur Bekämpfung der Reichweitenangst bei Elektrofahrrädern, einem der Hauptprobleme der Elektromobilität, geleistet. Die optimale Unterstützungsstrategie wurde bei bekannter Strecke und vorgegebener Akkukapazität mithilfe des CMSC-Verfahrens ermittelt. Dabei hat sich eine konstante Geschwindigkeit als optimal herausgestellt. Zusätzlich konnte festgestellt werden, dass die SoC-Trajektorie robust gegenüber Parameterunsicherheiten ist und selbst bei größeren Einflüssen nur minimal vom ursprünglichen Verlauf abweicht. In Simulationen und im Fahrversuch konnte gezeigt werden, dass die optimierte Fahrstrategie Vorteile gegenüber den herkömmlichen Fahrmodi aufweist. Hierbei konnte dieselbe Strecke bei gleichem Energieverbrauch über 10 % schneller absolviert werden. Aufgrund der vielen Einflussfaktoren ist eine pauschale Aussage hinsichtlich des Vorteils jedoch nicht möglich.
Für den Nutzer des Elektrofahrrads ist diese Ersparnis, im Vergleich zum sicheren Ankommen mit der zur Verfügung stehenden Akkukapazität, jedoch zweitrangig. Wie in der Diskussion angesprochen, sollten sich zukünftige Arbeiten mit der Umsetzung der hier durchgeführten Forschung auf dem Elektrofahrrad beschäftigen. Das Ziel sollte dabei ein neuartiger, optimierter Fahrmodus sein, der die Unterstützung in Abhängigkeit der geplanten Strecke und der verbleibenden Akkukapazität automatisch anpasst. Dadurch kann der Reichweitenangst entgegengewirkt werden. Dies sollte mit Nutzerstudien über einen längeren Zeitraum überprüft werden. Des Weiteren sollte untersucht werden, inwieweit die hier gewonnenen Erkenntnisse auf Elektrofahrzeuge anderer Bereiche übertragen werden können.
-

Autor
Dr.-Ing. Evgeny Lazutkin
Postdoc an der Fakultät für Informatik und Automatisierung, FG Prozessoptimierung, TU Ilmenau
-

Autor
Prof. Dr.-Ing. habil. Pu Li
Universitätsprofessor und Leiter des Fachgebiets Prozessoptimierung am Institut für Automatisierungs- und Systemtechnik, TU Ilmenau
-

Autor
Thomas Lipowsky, M.sc.
Vorausentwicklung, Bosch eBike Systems
-

Autor
Jan Schnee, M.Sc.
Vorausentwicklung, Inertialsensorik basierte Funktionen, Bosch eBike Systems
-

Autor
Dr. Jürgen Stegmaier
Systementwicklung, Bosch eBike Systems